Python ガウス基底関数フィッティング
Python ガウス基底関数フィッティング概要
ここまでで、マネーパートナーズ会員専用サイトにログインして
パートナーズ FX-チャート足情報サイトから豪ドル/円 日足情報をダウンロ-ドするファイルが完成しました。
引き続き、ダウンロ-ドした豪ドル/円 日足情報ファイルを利用していきます。
気温や株式の価格のような連続したデ-タがある時、これを数式で表現できると将来の値を予測するようなことができます。
過去Python 多項式フィッティングで予測
のなかで、多項式フィッティングを行うと、数値変化を関数化することができることを紹介しました。
今回は、ガウス関数を複数個使ってこれを足し合わせ、連続したデ-タを関数化したいと思います。
参考となる記述が
【機械学習】入門⑤ 線形基底関数モデル Pythonで学ぶ「教師あり学習」回帰編
にあります。
特に「線形基底関数モデル」の部分は重要ですので是非読んで見てください。
ガウス関数
ガウス関数は
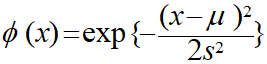
・・・・・①
のように書くことができます。
「μ」が分布の位置(中央値)を表しており、「s」がグラフの幅を表しています。
例えば、
func1 ⇒ μ=0, s=1
func2 ⇒ μ=1, s=1
func3 ⇒ μ=0, s=2
とすれば、その曲線は下図のようになります。
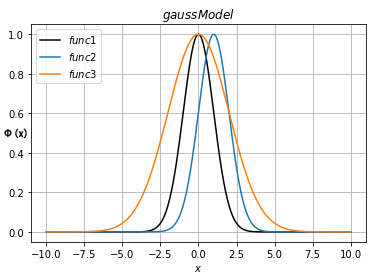
ガウス関数フィッティング
例えば x = 0~30 の31個からなるデ-タΦがあるときこれをガウス関数でフィッティングします。
ここでは簡単化のため4個のガウス関数でフィッティングします。
Φ0(x) から
Φ3(x) は中心μの異なるガウス曲線で
Φ4(x) は1とします。
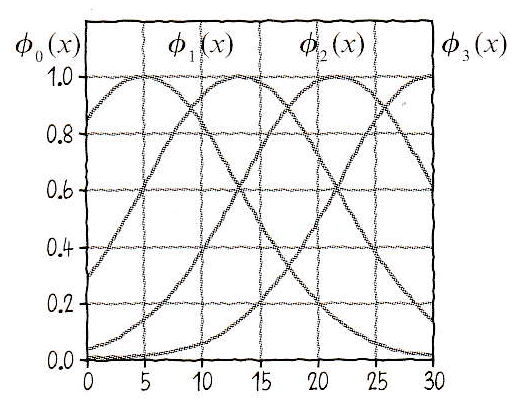
これらにそれぞれパラメ-タ W0から W3 を掛け合わせすべてを足し合わせた関数②を作成します。
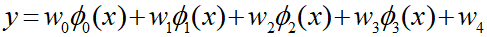
・・・・・②
これが、M = 4 のガウス基底関数モデルになります。
W0~W4 の値がわかれば y の値が決定されます。
例えば、
x = 0 の時 y = 0
x = 8 の時 y = 8
x = 16 の時 y = 10
x = 24 の時 y = 12
x = 30 の時 y = 12
だったとすれば、5次の連立方程式を解くことによって、5個の変数
W0~
W4
の値は決定することができます。
でもすべての 0~30 の x の値に関してその y の値が正しい値を示すとは限りません。
その各誤差の和が最小となるように微調整をする必要があります。
それでは、この問題を解いて行きたいと思います。
ガウス関数の定義
まずガウス関数①を定義します。
def gauss(x, mu, s): return np.exp(-(x - mu)**2 / (2 * s**2))
簡単に定義できました。
ガウス基底関数モデルの定義
次に、ガウス基底関数モデル②
def gauss_func(w, x):
を定義します。
w と x を与えると②式で計算した値を返してくれます。
- ガウス基底関数の数
ガウス基底関数の数は m は あらかじめ設定された M の値から、線形基底関数モデル厳密解・・・③[後述] を経由して m = M となって決定されます。
また、mu も③から決定され、w もあらかじめ、同じく③から求めておきます。 - 要素 0 の行列 y を作成
x と同じサイズで要素が 0 の行列 y を作成します。
y = np.zeros_like(x)
この中に、式②にしたがって計算した各 x に対応する y の値を代入します。
for j in range(m):
y = y + w[j] * gauss(x, mu[j], s)
y = y + w[m]
return y
ここまでをまとめると
# 線形基底関数モデル
def gauss_func(w, x):
m = len(w) - 1
xx = len(x) - 1
# y(x,w) = w0Φo(x) + w1Φ1(x) + w2Φ2(x) + w3Φ3(x) + w4
# なら len(w) = 5 ∴ m = 4
mu = np.linspace(0, xx, m)
s = mu[1] - mu[0]
y = np.zeros_like(x)
for j in range(m):
y = y + w[j] * gauss(x, mu[j], s)
y = y + w[m]
return y
となります。
ここまでで、ガウス基底関数モデルの定義の一部の設定が完了しました。
引き続き
ガウス基底関数モデル厳密解
def fit_gauss_func(x, t, m)
を定義します。