Python FFT & IFFT
Python FFT & IFFT 概要
Python で FFT と IFFT を探求してみたいと思います。
これからお話することについては、
Python で学ぶ WAV プログラミング(北山洋幸 著 第14,15章)
に詳しく書かれています、参考にされてください。
まずは、フ-リエ変換の基礎を超簡単に説明します。
フ-リエ変換は、時間軸上の連続した波形を周波数軸上に書換えます。
でも現実的にはデ-タは連続しているわけではなく、
毎日とか毎時とかいった不連続なサンプリングデ-タです。
すなわち離散的フ-リエ変換 DFT が用いられます。
FFT(Fast Fourier Tranform) 高速フ-リエ変換は
三角関数の周期性や対称性を利用した高速アルゴリズムを用いて
DFT を高速に処理します。
FFT の逆のことを行なうことを IFFT(Invers FFT) と呼びます。
これによって、ある信号に対して周波数軸上で処理することが可能なり、
処理後に IFFT で元の波形に戻すことができます。
簡単言えば、美容整形ですね。
例えば、高い周波数ノイズが乗った波形に対してロ-パス処理をすれば、ノイズを除去することができます。
Python FFT & IFFT の実際
実際に FFT を実行し、その後 IFFT を実行すると、元の波形に戻るのか確認します。
デ-タとしては、1が 10個、次に、0 が 44個、そして、1が 10個続く合計 64個のデ-タを用意します。
グラフ化すると下記のようになります。
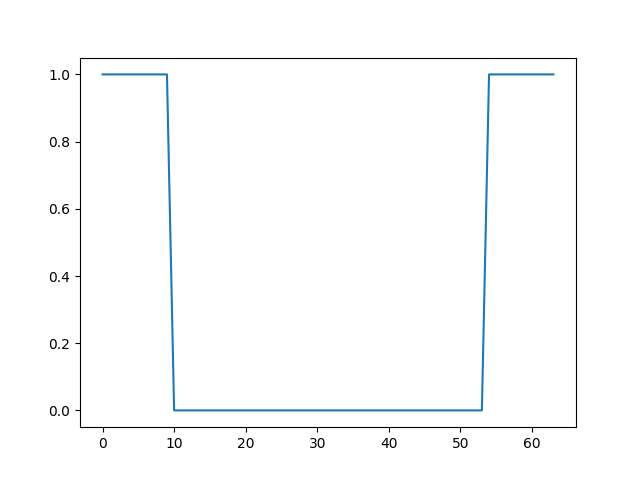
これに対して FFT を実行します。
実行結果は下記のようになります。
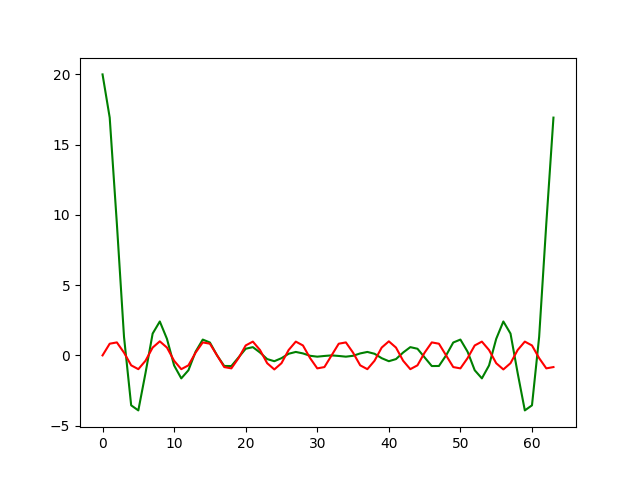
そして、FFT 結果に対して IFFT を実行すると FFT 実行前波形に戻ります。
ナイキスト周波数
FFT 処理を行なうプログラムが出力する結果は、中央のデ-タを軸として複素共役対称になっています。
共役複素数とは a+jb に対して a-jb となることです。
上図のFFT 結果をよく見てください。
X 軸が 32 のところが鏡となり、左右が対称になっていることが分かります。
これは、合計 64個のデ-タに対して FFT を実行したためです。
もっと簡単に言うと、FFT 後のデ-タは
(n/2)+1 点の情報を保持しておくだけで充分であることが分かります。
サンプリング数を N 個、その時のサンプリング周波数を f = N Hz とすると、
サンプリングに要する時間は 1 秒必要となります。
そして、FFT 解析ができる最大周波数は f/2 となります。
この f をナイキスト周波数(Nyquist frequency)と呼びます。
fnyq = f/2 = 32 Hz
となります。
逆に言うと、サンプリング周波数を高くしないと、高速波形の FFT 解析はできないことになります。
もう一度 FFT 実行結果の図を見てください。
サンプリング周波数を 64 Hz と仮定すると、X 軸の 0~64 の単位は 1 Hz です。
すなわち、元波形における 0~64 Hz の各周波数成分は 1 Hz ごとに分解して表示されます。
そして、0~32 Hz と 32 ~64 Hz の各周波数成分は 32Hz を境にして
左右が対称になっていることがわかります。
ここまでで、Python FFT & IFFT 概要 の説明が終わりました。
引き続き、ここまで説明してきたことが実行できる、最も単純な FFT & IFFT プログラムを作成します。