Python Colaboratory
時系列のためのディ-プラ-ニング
何とか Colab が使えるところまできました。
ここからは、時系列デ-タを使う機械学習について考えていきます。
時系列とは気温、株価、売上高、電力消費量など一定間隔の計測によって得られるデ-タのことです。
時系列関連のタスクのなかで最も一般的なのが予測です。
ここでは、
リカレント(再帰型)ニュ-ラルネットワ-ク(Recurrent Neural Network : RNN)
を使用して予測をしていきます。
RNN を理解する
RNN とはなんぞや訳がわからないというのが、勉強し始めた時の印象でした。
完璧にわかったかと言われると自信がないのですが、私が理解できたことを書いてみました。
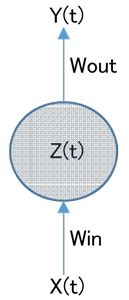
下図に、RNN の単純な構造を書いてみました。
ベクトル X(t) を入力として受取り、ある時刻 (t) にベクトル Y(t) を出力します。
簡単な例を上げて具体的に説明します。
ウィンドウ(シ-ケンス)を3として入力を3個ずつに区切ります。
t0 に x0
t1 に x1
t2 に x2
を入力として受取り ⇒ X(t)
t3 に x3
を出力 ⇒ Y(t)
したとします。
中央の円はネットワ-クの隠れ層(Dense)を表します。
入力重み行列を Win
出力重み行列を Wout
(Wout は活性化関数と呼ばれます)
とします。
そして、ベクトル Z(t) と呼ぶ隠れ層は一つしかないと仮定します。
このとき、
Z(t) = X(t) × Win
Y(t) = Z(t) × Wout
となりますので、
Y(t) = (X(t) × Win) × Wout
となります。
単純化するため
Win, Wout 行列は

のようにします。
とすると
Y(t)
= (x0×a0 + x1×a1 + x2×a2) × Wout
= x0×a0 + x1×a1 + x2×a2
となります。
a0, a1, a2 の値を求めてみましょう。
x0 = 0.5
x1 = 1
x2 = 2
x3 = 3
とします。
3 = 0.5 * a0 + 1 * a1 + 2 * a2
となります。
仮に、Win を Win-z ととし、その内容を
a0 = 0.2
a1 = 0.3
a2 = 0.5
とします。
このとき
Y(t) = 0.5 * a0 + 1 * a1 + 2 * a2
= 0.1 + 0.3 + 1
= 1.4
となります。
本当は 3 になって欲しいのでその微分値(傾き)は
δΔ = 3 / 1.4
= 2.143
各重み Win-z にこの δΔ をかけます。
すると新 an0~an2 は
an0 = a0 * 2.143 = 0.4286
an1 = a1 * 2.143 = 0.6429
an2 = a2 * 2.143 = 1.0715
となりますので、再度これを
Y(t) = x0×an0 + x1×an1 + x2×an2
に代入すると
Y(t) = 0.5 * 0.4286 + 1 * 0.6429 + 2 * 1.0715
= 0.2143 + 0.6429 + 2.143
= 3.000
となり何とか、a0~a2 の解 (an0~an2) を一式見つけることができました。
解が見つかれば、3個のデ-タ列から4番目の値を予測することができます。
この内容をまとめると次のようになります。
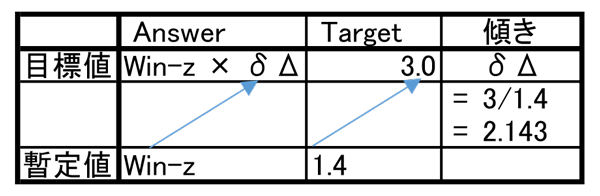
データ数が少ない時は簡単に解を見つけることができますが、データが多い時は難しくなります。
でも Keras を使用すると楽に見つけることができます。
引き続き、ここまでのところをまとめます。