Windows11 WSL2 Ubuntu Python Ⅱ

相関係数の応用

ここまでで前に戻る CSV データをスライシングし
sl_cl_t 配列[76×25]
を作成しました。
これに対して基準 kijyu 配列[1×20]を作成し、 sl_cl_t と kijyu の間の相関係数を求めます。

基準配列の作成
sl_cl_t 配列[76×25]の最後の20個を基準配列とします。
sl_cl_t の最後行は sl_cl_t[-1] で25個のデータがあります。
ここから最後の20個を抜き取ります。
kijyu = sl_cl_t[-1][5:]
または
kijyu = sl_cl_t[-1, 5:]
と書いても同じことになります。
比較配列の作成
基準 kijyu 配列は [1×20] ですので比較配列も[n×20]の書式になっている必要があります。
今相関を求めたい sl_cl_t 配列は[76×25]になっています。
これを後ろの５個ずつのデータを削除して比較 sl_cl_20 配列[76×20]に変換します。
sl_cl_20 = sl_cl_t[:,:20]
これで kijyu と sl_cl_20 は比較対象となりました。

相関係数の利用方法

ここまでで相関係数を計算するための準備はできたのですが、そもそも相関係数がわかるとどんな利点があるのでしょうか。
過去の実際のデータ列がわかるとこれから発生するデータを予測できます。
例えばジャンケンをするとき相手の出す手の順がわっかっていれば、次に出す手は予測できます。
グー、パー、グー、パー、グー、パーの順に出していれば、次はグーだろう考えるのが順当です。
x = 0.0, 0.1, 0.2, ････････ 9.7, 9.8, 9.9
の時
y = x + sin(x)
とするとそのグラフは下記の青線のようになります。

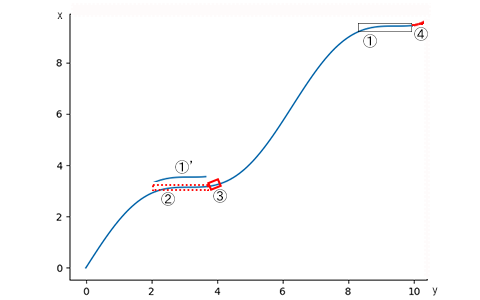
この時この先の
x = 10.0, 10.1, 10.2, 10.3, 10.4
の y の値を予測してみます。
y = x + sin(x)
を計算するのではありません。
あくまでも予測します。
どうすれば良いか考えます。
x = 8.0～9.9 の区間の y の値を、基準①とします。
①と相関する区間が x = 1.8～3.7 の区間の y の値に存在しこれを相関②とします。
相関②の先
x = 3.8, 3.9, 4.0, 4.1, 4.2
の区間の y の値が存在しこれを予測③とします。
③を平均値補正等をすると求める予測④になります。
このように相関性があることを見つけることができれば、未来を予測することができます。

相関係数の計算

話が横道にそれてしまいました。
本題に戻ります。
比較対象となった kijyu と sl_cl_20 の相関係数を求めます。
相関係数の求めかたについては
NumPy を使う-相関係数を求める
を参考にしてください。

相関係数 np.corrcoef(,)
kijyu と sl_cl_20 の相関係数 cor1 を求めます。
cor = np.corrcoef(kijyu, sl_cl_20)
print(cor)
cor1 = cor[1:, 0]
相関係数の最大値
相関係数の最大値 cor_max を求めます。
この値は１を超えることはありません。
cor_max = np.amax(cor1)
print('相関max=', cor_max)
この値は予測の信頼度を示す値になります。
cor_max = 1 ならば信頼度 100%
と言ってよいかもしれません。
相関係数最大 index
相関係数が最大となる index を求めます。
c_max_id = np.argmax(cor1)
print('相関max_ID=', c_max_id)
相関がとれた配列確認
相関がとれた配列を確認します。
print("相関する25個のデータ")
print(sl_cl_t[c_max_id])
グラフで表示します。
plt.plot(sl_cl_t[c_max_id]) # 相関する25個
plt.plot(kijyu) # ラスト20個
plt.show()

相関するデータのスケール補正

相関がとれた２つのデータのスケールを補正します。
sl_cl_20[c_max_id] と kijyu は相関がとれています。
予測値は
sl_cl_t[c_max_id] の中にあります。
一方、kijyu は
sl_cl_t[-1] の中にあります。
相関係数 np.corrcoef(,) は２つの配列のそれぞれの標準偏差値をとって比較しています。
よって sl_cl_t[c_max_id] の標準偏差値を計算し、この値を kijyu の標準偏差と平均値でスケール補正をします。
標準偏差値の計算方法については scikit-learn インストールの中で説明しました。
参考にしてください。

sl_cl_t[c_max_id]の標準偏差値
予測値 sl_cl_t[c_max_id] の標準偏差値を計算します。
必要となるライブラリをインポートします。
sklearn の中にある preprocessing モジュールが必要です。
from sklearn import preprocessing
インスタンスを作成します。
sscaler = preprocessing.StandardScaler()
標準化したいデータ準備
標準化したいデータを準備します。
標準化したいデータが１次元だと標準化してくれません。
sl_cl_t[c_max_id] を２次元に変換します。
x = sl_cl_t[c_max_id].reshape(-1,1)
標準偏差値を求める
標準偏差値 y は
y = sscaler.fit_transform(x)
print("sl_cl_t[c_max_id]標準偏差値")
print(y)
から求められます。
基準の標準偏差
相関の基準とした kijyu の標準偏差 s を求めます。
s = np.std(kijyu)
print("標準偏差 s = ", s)
基準の平均値
相関の基準とした kijyu の平均値 m を求めます。
m = np.mean(kijyu)
print("平均値 m = ", m)
予測値 sl_cl_t[c_max_id] スケール補正
sl_cl_t[c_max_id] の標準偏差値を kijyu の標準偏差 s と平均値 m で w にスケール補正します。
w = y * s + m
print("予測値 w = ", w)