Windows11 WSL2 Ubuntu Python Ⅱ
相関係数応用ファイルまとめ
ここまでで相関係数の応用について説明してきました。
引き続き、そのスクリプトの内容をまとめます。
# coding: utf-8
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
xl_df = pd.read_csv("public_html/manep-w/mane_chart_go.csv", encoding="cp932")
# print(xl_df)
Close = xl_df["終値(売り)"].values
Idx = xl_df.index
print(Idx)
print(Close)
print("Idx[-1]=", Idx[-1])
print("Idx[-24]=", Idx[-24])
n_25 = 25
sl_cl_t = []
for n in range(Idx[-24]):
sl_cl_t = np.append(sl_cl_t, Close[n:n+n_25]).reshape(n+1,n_25)
print("sl_cl_t")
print(sl_cl_t)
print(sl_cl_t.shape)
sl_cl_20 = sl_cl_t[:,:20]
print("sl_cl_20")
print(sl_cl_20)
# kijyu = sl_cl_t[-1][5:]
kijyu = sl_cl_t[-1, 5:]
print("基準値")
print(kijyu)
cor = np.corrcoef(kijyu, sl_cl_20)
print("cor")
print(cor)
cor1 = cor[1:, 0]
cor_max = np.amax(cor1)
print('相関max=', cor_max)
c_max_id = np.argmax(cor1)
print('相関max_ID=', c_max_id)
print("相関する25個のデータ")
print(sl_cl_t[c_max_id])
# print("基準")
# print(kijyu)
plt.plot(sl_cl_t[c_max_id]) # 相関する25個
plt.plot(kijyu) # ラスト20個
plt.show()
# インスタンスの作成
sscaler = preprocessing.StandardScaler()
x = sl_cl_t[c_max_id].reshape(-1,1)
print(" 元データsl_cl_t[c_max_id]を1×25 次元に変換")
print(x)
y = sscaler.fit_transform(x)
print("sl_cl_t[c_max_id]標準偏差値")
print(y)
# 基準 kijyu の標準偏差 s と平均値 m
s = np.std(kijyu)
print("標準偏差 s = ", s)
m = np.mean(kijyu)
print("平均値 m = ", m)
w = y * s + m
print("予測値 w")
print(w)
plt.plot(w) # 相関する25個
plt.plot(kijyu) # ラスト20個
plt.show()
# yamada@yama:~$ conda activate
# (base) yamada@yama:~$ python3 public_html/dsc-4.py
上記ファイルを windows 側で作成します。
上記内容をすべてをコピ-し、Python ファイルを作成します。
自分の PC Windows で TeraPad 等を使用して作成できたらファイル名を dsc-4.py として保存します。
文字コ-ドは、UTF-8N
BOM なし
改行コ-ドは、LF
です。
保存先はホスト Wimdows OS の
Linux \Ubuntu-22.04 \\wsl.localhost フォルダ
Linux/Ubuntu-22.04/home/yamada/public_html/dsc-4.py
とします。
相関係数応用ファイル動作確認
相関係数応用ファイルの動作確認をしていきます。
WSL2 Ubuntu のターミナルを立ち上げます。
立ち上げ方がわからない方は
Ubuntu の起動
を見てください。
yamada@yama:~$ conda activate
として conda 環境を有効にします。
public_html/dsc-4.py ファイルを実行します。
(base) yamada@yama:~$ python3 public_html/dsc-4.py
[結果]
RangeIndex(start=0, stop=100, step=1) [91.653 91.833 92.543 92.807 92.87 92.935 92.97 92.307 91.415 91.722 87.983 88.804 88.252 89.136 89.001 89.899 90.628 90.168 89.401 88.834 88.14 90.723 90.085 90.876 91.151 91.146 91.509 90.113 89.201 89.343 89.579 89.464 88.744 90.301 91.839 91.729 92.031 92.657 92.287 92.084 91.775 92.014 91.092 90.81 91.299 91.238 91.016 91.211 90.893 92.234 92.987 92.625 92.129 92.313 92.797 92.548 91.839 91.69 91.76 91.811 91.663 92.064 92.026 91.946 91.502 90.362 90.513 89.698 88.907 88.824 89.67 88.312 89.043 88.296 88.252 88.353 87.883 87.526 86.871 87.484 87.802 88.78 89.064 88.763 89.853 88.935 88.227 87.907 87.911 88.726 88.948 89.119 89.937 89.724 90.126 90.21 90.429 90.48 89.736 89.875] Idx[-1]= 99 Idx[-24]= 76 sl_cl_t [[91.653 91.833 92.543 ... 90.085 90.876 91.151] [91.833 92.543 92.807 ... 90.876 91.151 91.146] [92.543 92.807 92.87 ... 91.151 91.146 91.509] ... [88.296 88.252 88.353 ... 90.21 90.429 90.48 ] [88.252 88.353 87.883 ... 90.429 90.48 89.736] [88.353 87.883 87.526 ... 90.48 89.736 89.875]] (76, 25) sl_cl_20 [[91.653 91.833 92.543 ... 90.168 89.401 88.834] [91.833 92.543 92.807 ... 89.401 88.834 88.14 ] [92.543 92.807 92.87 ... 88.834 88.14 90.723] ... [88.296 88.252 88.353 ... 88.948 89.119 89.937] [88.252 88.353 87.883 ... 89.119 89.937 89.724] [88.353 87.883 87.526 ... 89.937 89.724 90.126]] 基準値 [87.802 88.78 89.064 88.763 89.853 88.935 88.227 87.907 87.911 88.726 88.948 89.119 89.937 89.724 90.126 90.21 90.429 90.48 89.736 89.875] cor [[ 1. -0.52161518 -0.41892202 ... 0.21974134 0.09783505 0.20264298] [-0.52161518 1. 0.83416821 ... -0.64466314 -0.60188009 -0.37970763] [-0.41892202 0.83416821 1. ... -0.77411074 -0.68357424 -0.64740369] ... [ 0.21974134 -0.64466314 -0.77411074 ... 1. 0.7412809 0.51627099] [ 0.09783505 -0.60188009 -0.68357424 ... 0.7412809 1. 0.77556036] [ 0.20264298 -0.37970763 -0.64740369 ... 0.51627099 0.77556036 1. ]] 相関max= 0.8540352988817729 相関max_ID= 22 相関する25個のデータ [90.085 90.876 91.151 91.146 91.509 90.113 89.201 89.343 89.579 89.464 88.744 90.301 91.839 91.729 92.031 92.657 92.287 92.084 91.775 92.014 91.092 90.81 91.299 91.238 91.016]元データsl_cl_t[c_max_id]を1×25 次元に変換 [[90.085] [90.876] [91.151] [91.146] ・・・・・・・・ [90.81 ] [91.299] [91.238] [91.016]] sl_cl_t[c_max_id]標準偏差値 [[-0.81116451] [-0.05658844] [ 0.20574838] [ 0.20097862] ・・・・・・・・ [-0.11954927] [ 0.34693328] [ 0.28874221] [ 0.07696485]] 標準偏差 s = 1.0093989213388341 平均値 m = 88.90675999999999 予測値 w [[88.08797142] [88.84963969] [89.11444219] [89.1096276 ] ・・・・・・・・ [88.78608709] [89.25695408] [89.19821607] [88.98444824]]
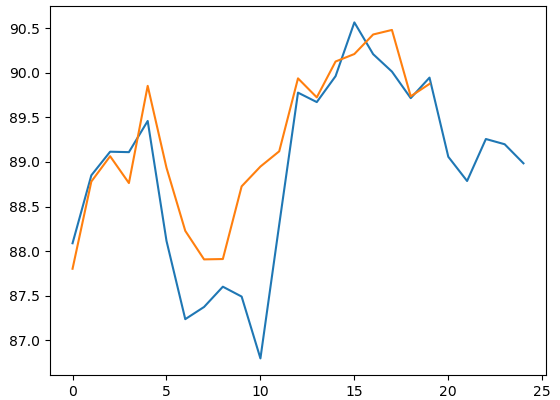
上記のように表示されれば完了です。
引き続きこのまま、元データをロ-ソク足表示にしてみます。